Para crear un brazo robótico hay que definir unos parámetros que se inventó un señor muy inteligente llamado Denavit-Hartenberg. Estos parámetros no son un simple invento sino que tienen su razón de ser y que explican muy bien en Wikipedia y son los más utilizados en robótica para diseñar eslabones en serie unidos por articulaciones.
Explicaremos detalladamente en qué consiste la definición de estos parámetros, cómo funcionan y desarrollan los movimientos que requerimos en el siguiente post “Referencias Denavit-Hartenberg“.
Para comenzar hay que entender que este convenio para definir parámetros es una simplificación de la descripción cinemática de un sistema en el que intervienen una serie de articulaciones.
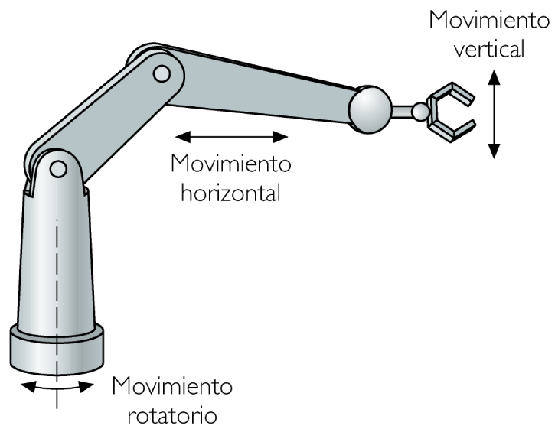
Supongamos un brazo que puede girar el hombro y el codo hasta la muñeca. Pues para mover la muñeca hasta una posición indicada es evidente que hay que mover las articulaciones anteriores desde el hombro que ha de levantar el codo y finalmente nuestra mano para poder saludar al vecino. A esto se le llama cinemática directa ya que existe una jerarquía de movimientos en la que el padre dominante es el hombro, y el codo y la muñeca sus hijas. Y de la misma manera el codo es padre de la muñeca.
Si intentáramos mover el hombro con un simple giro de muñeca sería algo impresionante.
En fin, esta cinemática está gobernada por la denominada composición de movimientos que de forma simple permite conocer como se mueve un punto B (codo) de nuestro brazo, conociendo el movimiento de otro punto A (hombro) y la relación de giro o traslación que hay entre ellos. De esta manera, si sabemos como se mueve el punto B (codo) que pertenece a otro eslabón (en este caso el antebrazo), podremos saber, como se mueve el punto C que es nuestra muñeca.
Pues con este ejemplo se puede aplicar la misma transformación a otro diseño de brazo y de manera sucesiva se pueden conocer todas las variables cinemáticas para ir más allá en robótica.
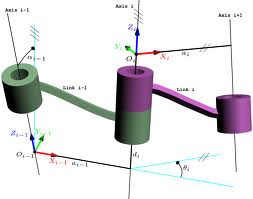
La mecánica clásica establece una serie de ecuaciones en la que se considera una referencia fija; en nuestro caso el hombro si suponemos que estamos parados; y otra referencia móvil que son las articulaciones siguientes. Por ello, hay que diseñar una serie de referencias con sus ejes (x,y,z) en cada articulación y siguiendo las instrucciones que indica el convenio de Denavit-Hartenberg, definir 4 parámetros que las relacionan.
Antes de que os aburráis de leer la explicación tediosa de lo que ocurre conceptualmente podéis visualizar este video que hace una introducción gráfica de cómo se aplica la definición de referencias y los parámetros de Denavit-Hartenberg.
Las articulaciones pueden ser rotacionales o prismáticas, osea que giran o se trasladan en una dirección. Y cada una de estas articulaciones sea del tipo que sea provee al sistema de un grado de libertad adicional. Y es recomendable no superar los 6 grados de libertad si se es inexperto, de esto ya hablaremos más adelante…
Podríamos utilizar otra manera de describir nuestro brazo, pero tendríamos un conjunto de ecuaciones incomestibles que para manipular puede resultar harto complicado.
El secreto de este método reside en el uso de matrices de transformación que son una definición unificada de una matriz del giro (3×3) y un vector de traslación (3×1), mientras que las ecuaciones de la mecánica habitual manipula estas componentes por separado. De esta manera simplificamos el problema y cuyos resultado podemos ver a continuación.
Una de las mejores maneras de entender cómo funciona este mundo de matrices de transformación es ver este tutorial de Udacity, que es el tema 4 de un curso interesante sobre gráficos 3D y es muy recomendable. Para que veáis que tiene mucha más aplicación que la robótica.

One comment