El concepto RAW que en inglés quiere decir en crudo, es la manera de decir que estamos recibiendo unos datos directamente del dispositivo, pero que aún no sabemos muy bien cómo interpretarlos.
Es cómo sacar oro de una mina, en la que hay que separar la piedra y otros metales mediante un proceso muy laborioso hasta conseguir oro puro.


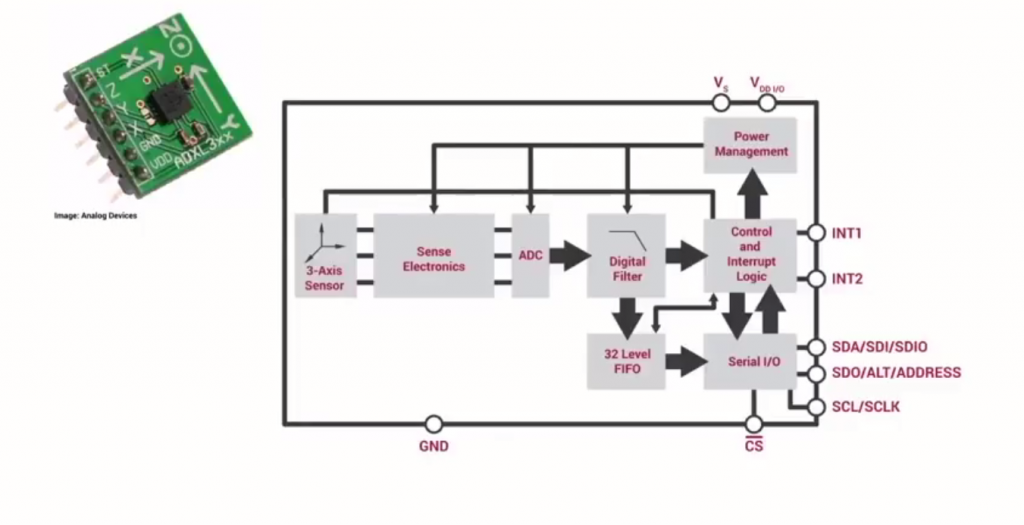
Un sensor IMU es un elemento muy complejo que contiene mucha más electrónica en su interior. Filtros, interrupciones, conversores… y aún así en pantalla nos aparecen unos números intratables.
Un componente que existe dentro de un IMU es lo que se denomina un DMP (Digital Motion Processor), que fusiona los datos del acelerómetro y del giroscopio para minimizar los efectos de los errores inherentes a cada sensor. El DMP calcula los resultados en términos de cuaterniones, y puede convertir los resultados en ángulos de Euler y realizar otros cálculos con los datos. Además integra un procedimiento de autocalibración. Esto quiere decir que nos ahorramos nosotros en programar el cálculo de error en el filtro de los valores que proporciona; aunque Invensense; los creadores de este dispositivo; no revelará el algoritmo que utilizan para combinar los datos.
Es por ello que vamos a realizar un primer ejercicio para obtener estas componentes, observaremos su salida y buscaremos distintos métodos para su correcta calibración y obtención de resultados.
Para empezar, deberemos conectar nuestro sensor MPU6050 o MPU9250 a través de los pines SDA y SCL en el pin A4 y A5 de nuestra placa Arduino.
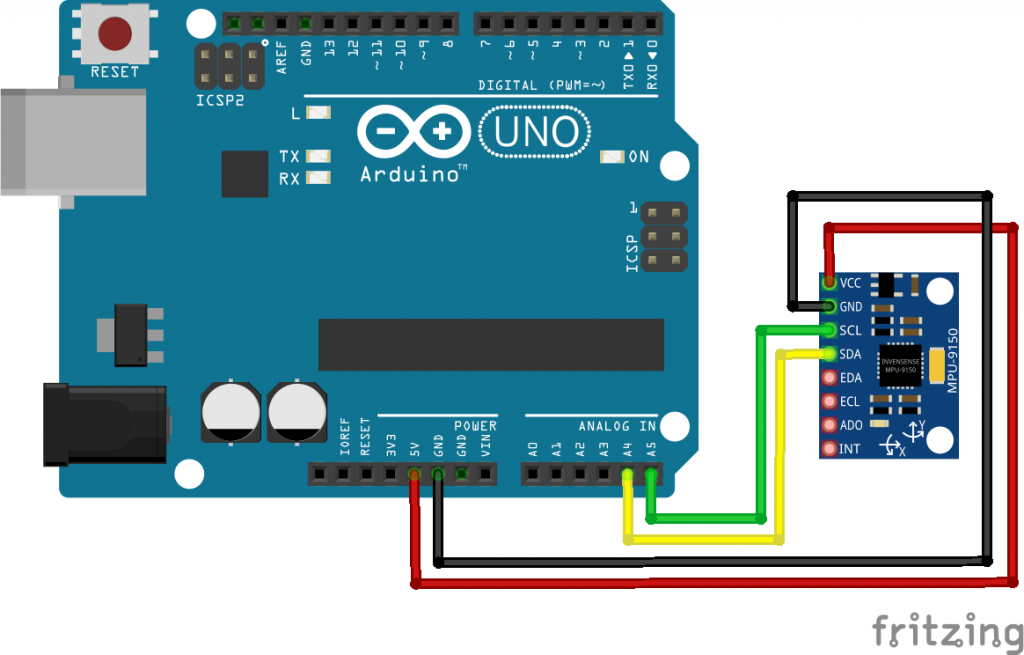
Esta conexión se hace a través de los pines I2C y requeriremos de la dirección I2C de nuestro sensor. Para estos sensores la dirección suele ser la 0x68 o la 0x71; pero en caso de no conocerla, podemos hacer un escaneado de direcciones que podéis buscar con el código de este enlace “Where is my I2C address?”.
Una vez hecho esto, debemos descargar la librería para hacer funcionar el sensor. En este momento, hago una pausa. Existen muchísimas librerías disponibles para este cometido, algunas complejas y otras más sencillas. Así que buscando la más simple y funcional he creado unas librerías propias, con las que seguro que estos sensores funcionarán y que se pueden descargar a través de los siguientes enlaces.
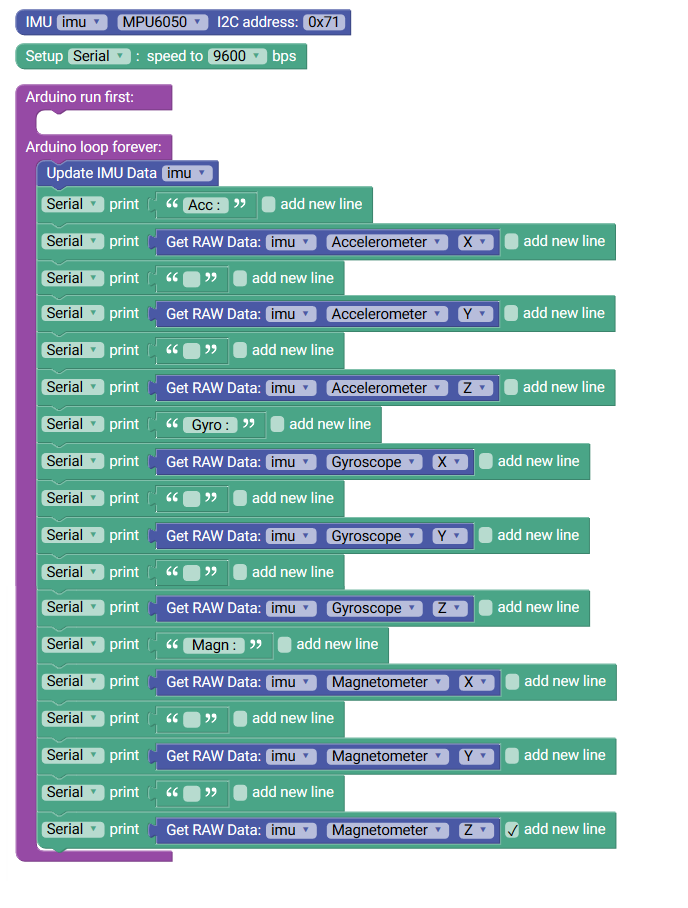
Este es el código para obtener valores de un sensor de 9 ejes MPU9250, para hacer funcionar un sensor MPU6050 de 6 ejes solo habrá que eliminar las 3 componentes del magnetómetro.
#include <IMU_MPU9250.h>
MPU9250 imu;
void setup() {
imu.calibrateMPU9250(imu.gyroBias, imu.accelBias);
imu.initMPU9250();
Serial.begin(9600);
}
void loop() {
imu.readAccelData(imu.accelCount);
imu.getAres();
imu.readGyroData(imu.gyroCount);
imu.getGres();
imu.readMagData(imu.magCount);
imu.getMres();
Serial.print("Acc : ");
Serial.print((float)imu.accelCount[0]*imu.aRes);
Serial.print((float)imu.accelCount[1]*imu.aRes);
Serial.print((float)imu.accelCount[2]*imu.aRes);
Serial.print(" Gyro : ");
Serial.print((float)imu.gyroCount[0]*imu.gRes);
Serial.print((float)imu.gyroCount[1]*imu.gRes);
Serial.print((float)imu.gyroCount[2]*imu.gRes);
Serial.print(" Magn : ");
Serial.print((float)imu.magCount[0]*imu.mRes);
Serial.print((float)imu.magCount[1]*imu.mRes);
Serial.println((float)imu.magCount[2]*imu.mRes);
}
Como se podrá observar, los números son bastante difíciles de tratar, especialmente porque en cada iteración del bucle loop, obtenemos 9 valores distintos, pero si no sabemos cómo se interpretan, ni cómo minimizar errores, es como no tener nada.
Por ello, hemos de utilizar unos filtros que nos ayudan a eliminar el ruido, los errores y manipular estos valores para obtener unos valores concretos de interés. La matemática contenida en estos filtros es bastante compleja y requiere de estudio que podéis consultar en la extensa información que proporcionan sus creadores.
*NO HACE FALTA ESTUDIARSE ESTOS FILTROS, ni crear librerías nuevas, ni hacer métodos raros que aparecen documentados en la profundidad de la web. Lo que necesitamos es una librería que aplique estos procedimientos para obtener nuestro objetivo y que veremos en la siguiente lección.
Si tenemos ansia por aprender, podemos buscar y poner a prueba todo lo aplicado por distintos autores e ivestigadores, pero nuestro tiempo es limitado y nuestro objetivo es muy específico.
Así que expongo algunos casos especiales que pueden ocurrir, pero a partir de aquí es cultura general de la tecnología.
Estos filtros tienen la siguiente misión:
- Minimizar errores de medida
- Evaluación de la tasa de cambio de las variables con el tiempo
- Obtener datos de valor en función de un sistema dependiente de estas magnitudes
Minimizar errores de medida
Los errores de medida que se pueden encontrar en las mediciones pueden deberse a:
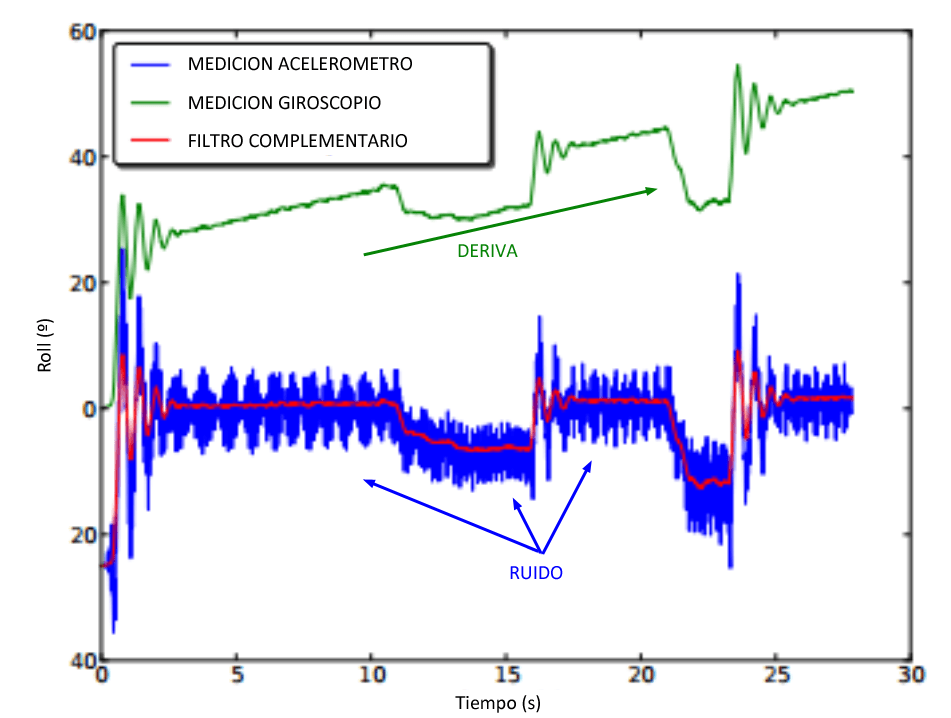
- Ruido (Noise) – En la electrónica, puede existir una componente que haga que la señal no sea limpia. Puede deberse a pequeñas corrientes magnéticas o una mala conexión que hacen que la amplitud de la señal no se vea claro. Se pueden caracterizar por su alta frecuencia y por su aleatoriedad. Para eliminar el ruido se utilizan filtros paso-bajo
- Deriva – La deriva (drift) es cuando el error no es constante en el tiempo, sino que se propaga y se hace más grande o más pequeño con la variación de la misma lectura del sensor. Lo más natural es restar el error constante para que no afecte durante todo el programa; como se puede observar en el siguiente post. Pero en este caso, hay que realizar otro tipo de corrección.
Estos casos se caracterizan por seguir un patrón determinado. Si hallamos ese patrón podríamos minimizar el ruido, pero no podemos predecir que el comportamiento sea siempre el mismo. Para ello, hay que ir calculando continuamente estas variaciones y corregirlas en tiempo real con respecto a medidas anteriores y así tendremos un sistema realimentado.
Las librerías publicadas con las que se leen estos datos disponen de funciones que aplican una calibración para limpiar esta deriva.
Evaluación de la tasa de cambio de las variables con el tiempo
Las variables obtenidas de los IMU, son variables temporales con las que se pueden obtener otras variables de estado del sistema.
Es decir, del acelerómetro, podríamos obtener la velocidad y la posición si integramos los valores obtenidos.
Del giroscopio que nos ofrece la velocidad angular, podemos integrar o derivar para obtener orientación o aceleración angular.
Esta puede ser la parte más compleja de las matemáticas utilizadas en estos filtros, ya que requieren de mediciones de tiempo en cada una de sus medidas y aproximan a estas ecuaciones derivativas para obtener resultados.
El caso que nos ocupa se extiende al uso de quaternions, así que mejor poner algún video explicativo, porque aquí la cosa se complica.
Si necesitáis más documentación al respecto, se puede acceder al pdf de cómo se aplica el filtro Madgwick; que es el filtro que utilizaremos para desarrollar todo este galimatías.
Obtener datos de valor en función de un sistema dependiente de estas magnitudes
Para hacernos una idea, sería un error valorar cada uno de los datos obtenidos de forma independiente.
Si tenemos el valor de 9 incognitas (incluso con menos), nuestra misión es buscar la combinación de las mismas para obtener un sistema de ecuaciones que despejando, nos proporcionen la información que requerimos.
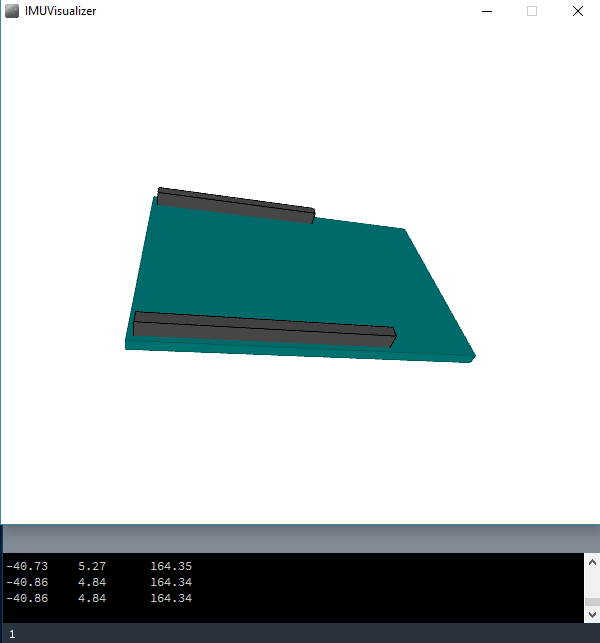
Para poder realizar la aplicación práctica de estos modelos, podemos pasar a la siguiente lección en la que podremos visualizar en un entorno tridimensional el comportamiento de este sensor y asegurarnos de que aplicamos bien las calibraciones y el cálculo de nuestras variables de estudio.