En este post voy a proponer un ejercicio relacionado con el diseño de piezas 3D mediante la API de Tinkercad.
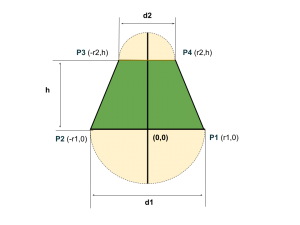
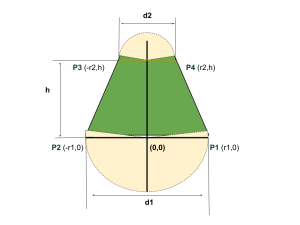
En el post anterior generábamos el contorno de una pieza en 2D que despues extruíamos para generar el modelo tridimensional como aparece en la siguiente figura.
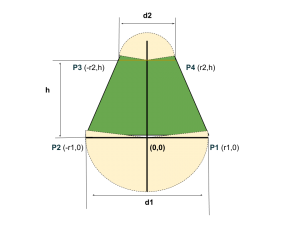
Pero el código que habíamos creado solo realizaba medias circunferencias y el resultado no es del todo limpio. Puesto que existe un escalón, queremos ahora crear una pieza con un contorno menos brusco como el que se ve anteriomente.
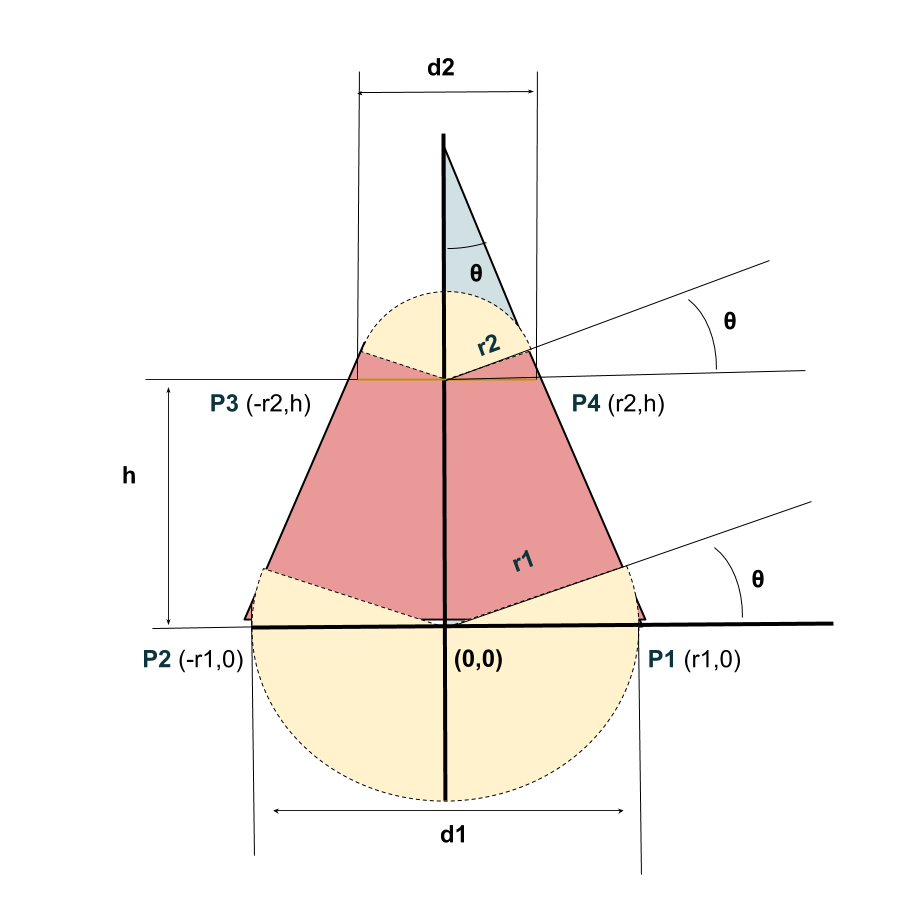
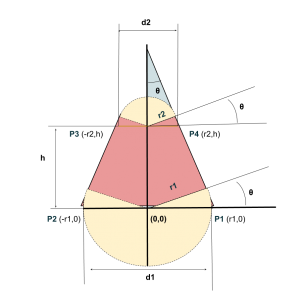
Este caso complica un poco más la generación de nuestra pieza ya que ahora las circunferencias abarcarán un angulo mayor o menor y los puntos que habremos de escoger no son los mismos cómo habíamos hecho anteriormente.
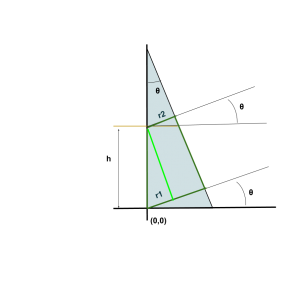
Ahora todo dependerá de un ángulo θ que está definido como la tangente entre estas dos circunferencias. Para el cálculo de este ángulo lo que hay que hacer es una operación dada la geometría de la pieza.
Sabemos por un lado que la tangente de un círculo es totalmente perpendicular a su superficie; por lo que sabemos que la recta que extiende este ángulo con respecto a los centros ha de ser perpendicular a la hipotenusa del triángulo.
Y lo mismo ocurrirá con el segundo círculo. Además también sabemos la distancia respectiva entre estos dos círculos.
De esta manera, si escogemos el triángulo interior que define el mismo ángulo en función de estos 3 parámetros; podremos calcular este ángulo aplicando una cuenta geométrica.
θ = atan(r1 -r2)/l
Ahora podremos aplicar todos los puntos en función de este ángulo; pero no acaba ahí la cosa. Tendremos que desarrollar una solución en distintos casos excepcionales que son los siguientes.
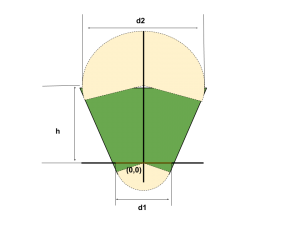
- Cuando el radio de la circunferencia superior es mayor que la inferior. r2>r1
- Cuando la suma de la longitud y el mínimo de los radios es menor que el mayor de los radios. l + min(r1,r2) < max(r1,r2)
En este caso, hay que tener en cuenta que si no existe un saliente sobre la figura, lo único que hay que crear es un cilindro cuyo diametro sea el mayor de los dos ; ya que se come el resto de la figura y queda definido en su interior. Esta excepción queda representada en la siguiente figura.
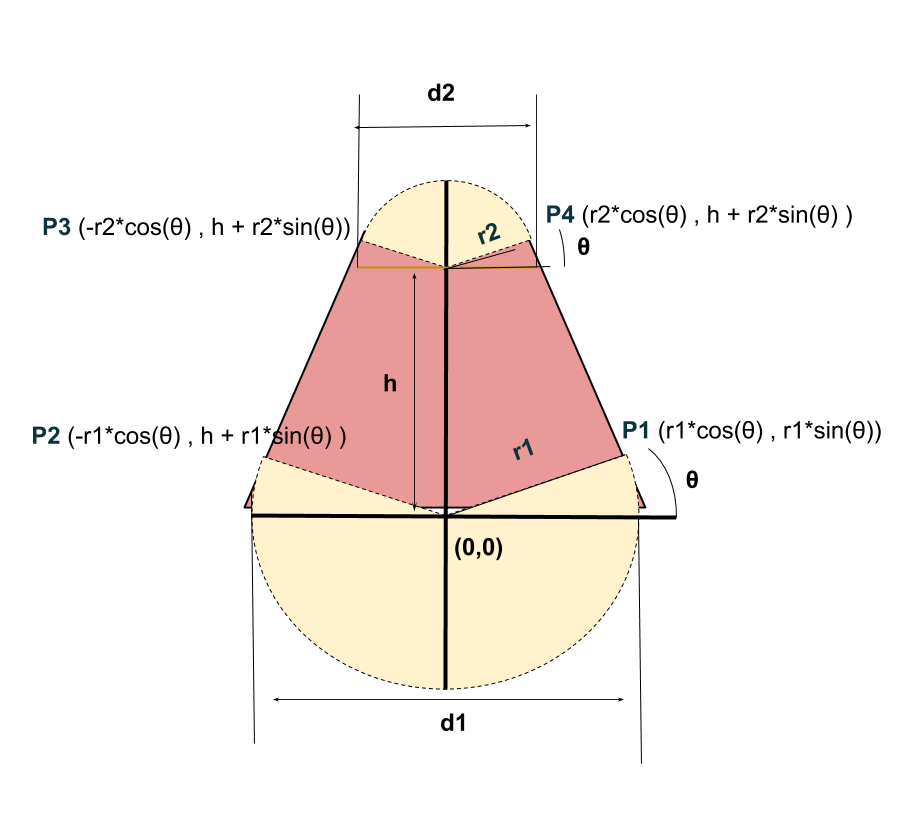
Una vez que tengamos en cuenta estas posibilidades hay que establecer cuales son los puntos que vamos a definir; ya que ahora las coordenadas tendrán una dependencia con este ángulo nuevo.
Hay que tener en cuenta que estas coordenadas de los puntos pueden cambiar si el radio mayor pasa a ser el menor, de tal manera que los senos quedarían en negativo; así que lo que hacemos es definir un factor de 1 positivo o negativo; y en el caso de que ocurra sumar o restar esa componente con la misma función.
De esta manera podemos crear el siguiente código:
var Path2D = Core.Path2D;
var Mesh3D = Core.Mesh3D;
var Tess = Core.Tess;
var Solid = Core.Solid;
var Debug = Core.Debug;
var Generator = {
parameters: function(callback) {
var params = [
{ "id": "r1", "displayName": "Top radius", "type": "float", "rangeMin": 1, "rangeMax": 100, "default": 15.0 },
{ "id": "r2", "displayName": "Bottom radius", "type": "float", "rangeMin": 1, "rangeMax": 100, "default": 10.0 },
{ "id": "length", "displayName": "Length", "type": "float", "rangeMin": 1, "rangeMax": 100, "default": 20.0 }
];
callback(params);
},
evaluate: function(params, callback) {
var path = new Path2D();
//Parameters
var r1 = params["r1"];
var r2 = params["r2"];
var l = params["length"];
var pi2 = 2.0 * Math.PI;
if (l+Math.min(r1,r2)<Math.max(r1,r2)){
Debug.log("Error Exception: This parameters define a cylinder with the maximum radius parameter");
var r = Math.max(r1,r2);
var lod = Tess.circleDivisions(r);
var step = (pi2)/ lod;
path.moveTo(r,0);
for(var d = 0; d < pi2; d += step) {
path.lineTo(Math.cos(d)*r, Math.sin(d)*r);
}
}else{
var theta = 0;
theta = Math.atan((Math.max(r1,r2)-Math.min(r1,r2))/l);
//Factor definition for senoidal orientation
var factor = 1;
if (r2>r1){
factor = -1;
}
//Debug.log(theta*360/pi2);
var lod1 = Tess.circleDivisions(r1);
var step1 = (pi2 + 2*theta*factor )/ lod1;
var lod2 = Tess.circleDivisions(r2);
var step2 = (pi2 - 2*theta*factor )/ lod2;
path.moveTo(-r1*Math.cos(theta),r1*Math.sin(theta));
for(var a = pi2/2-factor*theta; a < pi2+factor*theta; a += step1) {
path.lineTo(Math.cos(a)*r1, Math.sin(a)*r1);
}
path.lineTo(r1*Math.cos(theta),factor*r1*Math.sin(theta));
for( a = factor*theta; a < pi2/2-factor*theta; a += step2) {
path.lineTo(Math.cos(a)*r2, Math.sin(a)*r2+l);
}
path.lineTo(-r2*Math.cos(theta),l+factor*r2*Math.sin(theta));
path.lineTo(-r1*Math.cos(theta),factor*r1*Math.sin(theta));
path.close();
}
var solid = Solid.extrude([path], 20);
var mesh_piece = solid.mesh;
var s = Solid.make(mesh_piece);
callback(s);
}
};
// Returns the object-oriented shape generator,
function shapeGenerator() {
return Generator;
}